Emotional Arcs and Random Diffusion

There are some PCA tutorials online. I recommend the one by Jon Shlens (arXiv: 1404.1100). In brief, PCA provides a representation of the original data that is easier to understand. PCA reveals patterns that are hidden due to noise, redundancy, and improper "point of view" onto the data. The result of the PCA is a set of dimensions (vectors) - so-called principal modes that re-represent the input data in the best way (no matter what exactly "the best" means). One can visualize the input data using the principal modes obtaining so-called principal components (PCs). In other words, PCA allows emphasizing the most important "directions" or patterns of the original data.

Recently, researchers from University of Vermont, USA, and University of Adelaide, Australia, published a story about stories (arXiv: 1606.07772). They took about 1,300 books of fiction available on the Project Gutenberg, and one book by one they analyzed how the mood is changing throughout the story. The way, it was done, scores certain words according to their emotional impact. As a result, they obtained an x-y plot for each of the books, where the x-axis describes the timeline (or progress) of the story, and the y-axis corresponds to the bad-good emotional scale. Such a plot is called emotional arc and using PCA they found the most common emotional arcs. Here is an example of Alice's Adventures in Wonderland by Lewis Carroll taken from http://hedonometer.org.

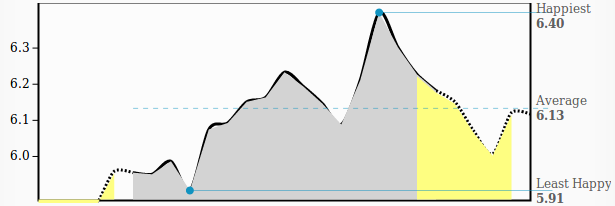
There have been a couple of blog posts published already, often appreciating Kurt Vonnegut's contribution (see MIT Technology Review or No Film School). I'd like to highlight another aspect of the study. First, I should mention a bit about random diffusion though.

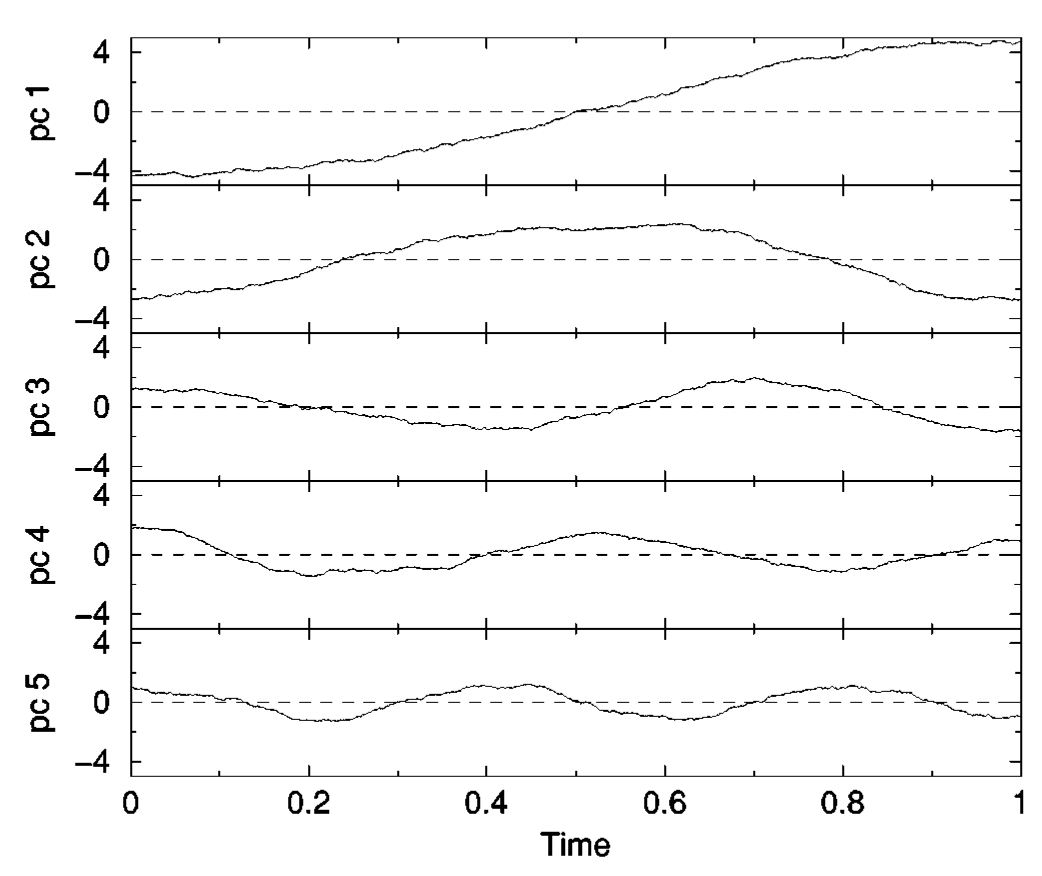
Berk Hess found an important feature of PCA. In two Phys. Rev. E papers (PRE.62.8438, PRE.65.031910) he explained that for a multi-dimensional random walk PCA provides cosine-like principal components. This finding is rather counter-intuitive; there is no significant pattern in the original data (the data is "generated" by a random process indeed), and still, PCA suggests some of the directions are preferred, or more suitable for the description of the data. The figure below shows the first six PCs of a 120-dimensional random walk.

Going back to the emotional arcs, the researchers claim to reveal using PCA six main arcs. They resemble, what a surprise, cosines. The figure below shows the first three PCs (orange) and the closest stories to each.

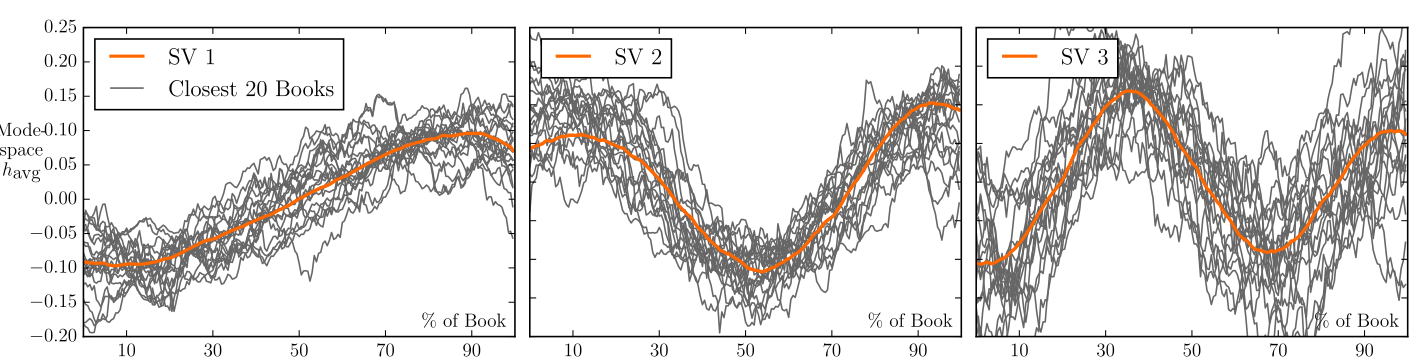
Of course, it may still be that a sort of randomness of the original data, or lack of convergence of the analyses is emerging from the PCA. Fortunately, the reasoning is unidirectional: random process generate cosine-like PCs indeed, but there is no guarantee that what looks cosine-like must be random. It may be that people simply like stories that look like cosines. After all, our lives look exactly like this: ill fortune, good fortune, repeat.